_________________________________________________________________________________________________________
Enumerated types

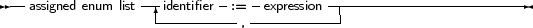
___________________________________________________________________
With the exception of int64, qword and Real types, all base types are ordinal types. Ordinal types have the following characteristics:
A list of pre-defined integer types is presented in table (3.1).
| Name |
| Integer |
| Shortint |
| SmallInt |
| Longint |
| Longword |
| Int64 |
| Byte |
| Word |
| Cardinal |
| QWord |
| Boolean |
| ByteBool |
| WordBool |
| LongBool |
| Char |
The integer types, and their ranges and sizes, that are predefined in Free Pascal are listed in table (3.2). Please note that the qword and int64 types are not true ordinals, so some Pascal constructs will not work with these two integer types.
| Type | Range | Size in bytes |
| Byte | 0 .. 255 | 1 |
| Shortint | -128 .. 127 | 1 |
| Smallint | -32768 .. 32767 | 2 |
| Word | 0 .. 65535 | 2 |
| Integer | either smallint or longint | size 2 or 4 |
| Cardinal | longword | 4 |
| Longint | -2147483648 .. 2147483647 | 4 |
| Longword | 0 .. 4294967295 | 4 |
| Int64 | -9223372036854775808 .. 9223372036854775807 | 8 |
| QWord | 0 .. 18446744073709551615 | 8 |
The integer type maps to the smallint type in the default Free Pascal mode. It maps to either a longint in either Delphi or ObjFPC mode. The cardinal type is currently always mapped to the longword type.
Remark: All decimal constants which do no fit within the -2147483648..2147483647 range are silently and automatically parsed as 64-bit integer constants as of version 1.9.0. Earlier versions would convert it to a real-typed constant.
Free Pascal does automatic type conversion in expressions where different kinds of integer types are used.
Free Pascal supports the Boolean type, with its two pre-defined possible values True and False. These are the only two values that can be assigned to a Boolean type. Of course, any expression that resolves to a boolean value, can also be assigned to a boolean type.
| Name | Size | Ord(True) |
| Boolean | 1 | 1 |
| ByteBool | 1 | Any nonzero value |
| WordBool | 2 | Any nonzero value |
| LongBool | 4 | Any nonzero value |
Free Pascal also supports the ByteBool, WordBool and LongBool types. These are of type Byte, Word or Longint, but are assignment compatible with a Boolean: the value False is equivalent to 0 (zero) and any nonzero value is considered True when converting to a boolean value. A boolean value of True is converted to -1 in case it is assigned to a variable of type LongBool.
Assuming B to be of type Boolean, the following are valid assignments:
Boolean expressions are also used in conditions.
Remark: In Free Pascal, boolean expressions are by default always evaluated in such a way that when the result is known, the rest of the expression will no longer be evaluated: this is called short-cut boolean evaluation.
In the following example, the function Func will never be called, which may have strange side-effects.
Here Func is a function which returns a Boolean type.
This behaviour is controllable by the {$B } compiler directive.
Enumeration types are supported in Free Pascal. On top of the Turbo Pascal implementation, Free Pascal allows also a C-style extension of the enumeration type, where a value is assigned to a particular element of the enumeration list.
_________________________________________________________________________________________________________
Enumerated types

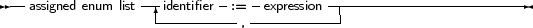
___________________________________________________________________
(see chapter 9, page 337 for how to use expressions) When using assigned enumerated types, the assigned elements must be in ascending numerical order in the list, or the compiler will complain. The expressions used in assigned enumerated elements must be known at compile time. So the following is a correct enumerated type declaration:
A C-style enumeration type looks as follows:
As a result, the ordinal number of forty is 40, and not 3, as it would be when the ’:= 40’ wasn’t present. The ordinal value of fortyone is then 41, and not 4, as it would be when the assignment wasn’t present. After an assignment in an enumerated definition the compiler adds 1 to the assigned value to assign to the next enumerated value.
When specifying such an enumeration type, it is important to keep in mind that the enumerated elements should be kept in ascending order. The following will produce a compiler error:
It is necessary to keep forty and thirty in the correct order. When using enumeration types it is important to keep the following points in mind:
will, when run, print the following:
More information can be found in the Programmer’s Guide, in the compiler directives section.
A subrange type is a range of values from an ordinal type (the host type). To define a subrange type, one must specify its limiting values: the highest and lowest value of the type.
_________________________________________________________________________________________________________
Subrange types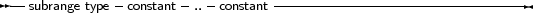
___________________________________________________________________
Some of the predefined integer types are defined as subrange types:
Subrange types of enumeration types can also be defined: